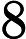D3Q27 - Single phase flow
Before start, it is assumed that the reader is already familiar with:
- Basic model creation in the TCLB code, see first tutorial.
- Basics of the LB physics, see obligatory SRT LBM tutorial.
- Basics of running TCLB
We will cover following topics:
- Importing a txt geometry image
- Simulating 3D flow through the geometry
- Using convergence criteria in TCLB
- Determining the permeability of the imported geometry
This tutorial looks to benchmark a three-dimensional single phase model in TCLB with the porous media test cases from:
Andrä et al. (2013). Digital rock physics benchmarks - Part I: Imaging and segmentation, Computers & Geosciences 50, 25-32.
Andrä et al. (2013). Digital rock physics benchmarks - Part II: Computing effective properties, Computers & Geosciences 50, 33-43.
In particular, we will look at the Fontainebleau sandstone sample and assess its permeability in x-, y- and z-directions. The permeability of a sample typically tells us how 'easy' it is for a fluid to flow through it, making it a very useful measurement for example in the determining extraction feasiblity of natural resources from underground reservoirs.
Downloading the geometry
In this tutorial, the permeability of a sandstone sample will be determined. The image for this was made available by the authors and can be downloaded from:
https://github.com/fkrzikalla/drp-benchmarks
In this repository, the specific image we are after can be found in /images/fontainebleau/segmented-exxon.raw.gz. The first problem that we must overcome in this tutorial is that the image compressed inside this folder consists of the full Fontainebleau sample in uint8 format. To make this useable with TCLB we need to convert the format type and ordering of the file that we wish to use for permeability testing. In order to do this,
- Extract data from .raw.gz, this can be done with applications such as 7zip or other default programs. Extracting this will place a file 'model.raw' into your directory.
- In your TCLB working directory create:
- Extract the subset noting that this is in python indexing. To do this, make a new python script in my/fontainePerm:
mkdir my
mkdir my/fontainePerm
import numpy as np
input_File = r'model.raw'
output_File = r'model.dat'
dat = np.fromfile(input_File, dtype='uint8')
dat = np.where( dat > 0.5, 1, dat)
print("Porosity prediction = %.4f" % ( 1.0-sum(dat)/float(len(dat)) )
nx = int(288)
ny = int(288)
nz = int(300)
dat = np.reshape(dat, (nx, ny, nz), order = 'F').swapaxes(0,1)
with open(output_File, 'w') as outfile:
counter = 0
percent = 0
for mySlice in dat:
if (counter % int(nx/5)) == 0:
print("Progress check... %d %% " % (percent) )
precent += 20
counter +=1
np.savetxt(outfile, mySlice, fmt="%d")
Building the model
Having constructed our model geometry file for TCLB, we can create the run file for our case inside of my/fontainePerm/. To start this off, we will generate a gauge set of units such that our output results will be physical rather than in lattice units. To do this:
<?xml version="1.0"?>
<CLBConfig version="2.0" output="output/fontaine/">
<Units>
<Param value="7.5e-6m" gauge="1" />
<Param value="1e-6m2/s" gauge="0.1666667"/>
<Param value="1000kg/m3" gauge="1"/>
</Units>
<Geometry>
</Geometry>
<Model>
</Model>
<Solve>
</Solve>
</CLBConfig>
Here, the units have been set based on the CTimage taken having a resolution of 7.5e-6m and the fact that we will be flowing a water-type fluid through the sample, so the viscosity and density are chosen to reflect this. Additionally, above can be seen that placeholders have been set for the other parameters required for the TCLB input file.
The next stage consists of setting up the simulation geometry. Here, we have to import the .dat file previously created and tell TCLB that these are wall geometries. In addition to this, we want to have an inlet and outlet reservoir, so the imported geometry must be placed with this in mind. For this, the Geometry flag above can be specified:
<Geometry nx="320" ny="288" nz="300">
<MRT><Box/><MRT>
<Wall mask="ALL">
<Text file="./my/fontainePerm/model.dat" dx="16" nx="288" ny="288" nz="300" />
</Wall>
<Body mask="ALL">
<Text file="./my/fontainePerm/model.dat" dx="16" nx="288" ny="288" nz="300" />
</Body>
</Geometry>
Note that we have created the geometry with the Wall boundary flag, but as we intend to use the d3q27_cumulant model, we have also specified the geometry with the ADDITIONALS flag of Body. The d3q27_cumulant model uses this flag and attempts to calculate the drag in all directions on it. This ADDITIONALS flag is not essential for this tutorial as one can use a force balance technique to work out the drag on the solid body, but provides an example of how additional flags can be used. With the geometry file imported, we now set the viscosity in the model to 1e-6m2/s and the force pushing the fluid through the domain as 0.981m/s2. Linking this with normal output operations gives the final file as:
<?xml version="1.0"?>
<CLBConfig version="2.0" output="output/fontaine/">
<Units>
<Param value="7.5e-6m" gauge="1" />
<Param value="1e-6m2/s" gauge="0.1666667"/>
<Param value="1000kg/m3" gauge="1"/>
</Units>
<Geometry nx="320" ny="288" nz="300">
<MRT><Box/><MRT>
<Wall mask="ALL">
<Text file="./my/fontainePerm/model.dat" dx="16" nx="288" ny="288" nz="300" />
</Wall>
<Body mask="ALL">
<Text file="./my/fontainePerm/model.dat" dx="16" nx="288" ny="288" nz="300" />
</Body>
</Geometry>
<Model>
<Param name="nu" value="0.1666667"/>
<Param name="ForceX" value="0.981m/s2"/>
</Model>
<Solve Iterations="50000">
<VTK Iterations="10000"/>
<Failcheck Iterations="1000"/>
<Stop FluxChange="1e-3" Times="2" Iterations="1000"/>
</Solve>
</CLBConfig>
Note here that we have also indicated a stop checker in the xml file. This flag checks the global Flux for a change less than 1e-3. If this happens twice in a row than the simulation will also stop based on convergence. The global Flux is currently calculated inside of the CollisionMRT() function in models/flow/d3q27_cumulant/Dynamics.c.Rt as:
AddToFlux( getU_().x );
As this is only in the x-direction, we will adjust this to 'getU_().y' and 'getU_().z' when assessing the permeability in these directions.
Running the simulation
As previously mentioned, the d3q27_cumulant model will be used for this tutorial, as such from your TCLB directory run:
make -j 8 d3q27_cumulant
With the size of this model, it is recommended to run the simulation on a cluster or GPU if you can (otherwise you may be in for a bit of a wait). To reduce the wait time, one can relax the convergence criterion e.g. FluxChange="0.1". However, this can reduce the accuracy of the permeability prediction. An example of the slurm file used to run this tutorial on The University of Queensland's Goliath facility is:
#!/bin/bash
#SBATCH --ntasks=2
#SBATCH --ntasks-per-node=2
#SBATCH --partition=gpu
#SBATCH --gres=gpu:2
#SBATCH --job-name="Perm Test"
#SBATCH --output=$HOME/TCLB/output/fontainte/out.%6j
#SBATCH --error=$HOME/TCLB/output/fontainte/err.%6j
module load mpi/oopenmpi-x86_64
echo "Job: \${SLURM_JOB_NAME}"
nvidia-smi
mpirun $HOME/TCLB/CLB/d3q27_cumulant/main my/fontainePerm/fontaineExample.xml
On two GPU's the code converged at around 47000 iterations and takes approx. 35 minutes to compute.
Post-processing
In order to analyse the data, we will take advantage of Paraview's python package. Note that this can also be done with Paraview, but the vtk package can be useful for a number of scenarios or for processing of larger files and larger file numbers. The required analysis consists of:
- Integrate the velocity field and determine the porosity of the extended domain
- Determine the average velocity
- Calculate the superficial velocity
- Use a force balance to predict the drag force on the solid
- Calculate the permeability
The following python code indicates how this can be done:
from paraview.simple import *
file = r'./output/fontaine/fontaineExample_VTK_P00_00050000.pvti' #note that this will need to be adjusted to your final timestep
myFile = XMLPartitionedImageDataReader(FileName=file)
myThreshold = Threshold(Input=myFile)
myThreshold.Scalars = ['CELLS', 'BOUNDARY']
myThreshold.ThresholdRange = [0.0, 0.5]
integrateVars = IntegrateVariables(Input=myThreshold)
myData = paraview.servermanager.Fetch(integrateVars).GetCellData()
U = myData.GetArray('U').GetValue(0)
Fluid = myData.GetArray('Volume').GetValue(0)
#Divide U by volume to get average velocity:
rho = 1000 #kg/m3
nu = 1e-6 #m2/s
Force = 0.981 #m/s2
dx = 7.5e-6
lx = 320*dx
ly = 288*dx
lz = 300*dx
vol = lx*ly*lz
U_avg = U/vol
poro = Fluid/(vol)
U_super = U_avg * (1-poro)
F_d = vol * (1-poro) * rho * Force
DarcyFactor = 9.869233e-16
perm = vol * rho * nu * U_super / (F_d * DarcyFactor) #mD
print("Sample permeability is %f mD" % (perm))
The above should give you a permeability of around 1575mD. From here, the process above can be completed in the y and z directions with the following points to remember:
- The convergence criterion is currently based on x-direction velocity, if you want to use this criterion it is best to edit the Dynamics.c.Rt file to include y and z velocities in the Flux
- An inlet and outlet reservoir have been used in the x-direction here, this will need to be translated to the relevant direction
From doing this, you should find permeabilities around 1800mD in the y and 1900mD in the z.
References
Tip
A good starting point explaining the 'zoology' of various LBM models is a modern (2017) book 'The Lattice Boltzmann Method: Principles and Practice' written by T. Krüger, H. Kusumaatmaja, A. Kuzmin, O. Shardt, G. Silva, E.M. Viggen .
-
LINK TO THE GIT PAGE FOR THE GEOMETRY ↩