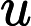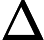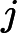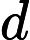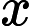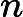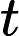Finite difference wave equation

These tutorials will try to teach you how to make and use a new model in TCLB. First it will discuss our goal: the model we want to create. Then it will take you step by step, on how to create all the needed components.

Finite difference wave equation

We want to discretize the Wave Equation:

$$\ddot{u} = c^2\Delta u$$

For this purpose we will use Finite Difference method. First we change the equation into two first order (in time) equations:

$$\left\{\begin{eqnarray} \dot{v} = &c^2\Delta u \\ \dot{u} = &v \end{eqnarray}\right.$$

Now let us discretise the Laplace operator with simple finite difference (in 2D):

$$\Delta u \approx \frac{(u_{i-1,j}+u_{i+1,j}+u_{i,j-1}+u_{i,j+1}-4u_{i,j})}{(dx^2)}$$

Finnaly we will use, what is called Semi-implicit Euler rule to integrate this equation in time. This will give us:

$$\left\{\begin{eqnarray} v^{n+1}_{i,j} &= v^n_{i,j}+dt c^2\Delta u^n \\ u^{n+1}_{i,j} &= u^n_{i,j} +dtv^{n+1}_{i,j} \end{eqnarray}\right.$$

The semi-implicit-ness can be seen in the index of v in the second line

Finnaly: we will get rid of all units by assuming dx and dt equal to 1

Implementation

Creating a model

Every model in TCLB is defined by a subdirectory of models. Let us now create a new one:

mkdir models/tutorial/wave
touch models/tutorial/wave/conf.mk

The conf.mk file stores some additional settings for a model, but it also tells TCLB that this directory is in fact a model.

Now we have to add two main files defining everything: Dynamics.R - defining all the setup of the model, and Dynamics.c - defining what will be happening in a node.

touch models/tutorial/wave/Dynamics.R
touch models/tutorial/wave/Dynamics.c

We want to have two Fields: u and v. We define them in Dynamics.R:

AddField(name="u")
AddField(name="v")

Then we need the main dynamics of a node. First let us write down the functions that will be used in the model(in Dynamics.c):

CudaDeviceFunction float2 Color() {
  float2 ret;
  ret.x = 0;
  ret.y = 1;
  return ret;
}

CudaDeviceFunction void Init() { }

CudaDeviceFunction void Run() { }

The CudaDeviceFunction prefix is needed for all functions in Dynamics.c for technical reasons. We needed to fill only the Color function, as it is the only one which returns a value. For now, the model doesn't do much. Before continuing, let us first understand what these function do:

Function	Description
Init	This function is called in all the nodes at the beginning of the simulation. All the initialization happens here.
Run	This function will be called in every node in every iteration - it is the main dynamic of a node.
Color	This function is useful only for the version of CLB with enabled graphics(./configure --enable-graphics). It calculates the level x on which the color of a pixel will be based. In most cases this will be temperature or velocity.

First dynamics

First, we want to initialize our fields(Dynamics.c):

CudaDeviceFunction void Init() {
  u = 0;
  v = 0;
}

Then let us start with a model that just preserves both fields without changing them. In TCLB we access fields with a notation u(dx,dy), where dx and dy is the position from which to take the field, relative to the current node(Dynamics.c):

CudaDeviceFunction void Run() {
  u = u(0,0);
  v = v(0,0);
}

Adding Quantities

Finally we want to access the resulting data. In TCLB, the data that will be exported to VTK, TXT or other format, are called [[Quantities]]. Let us add a quantity U to Dynamics.R:

AddQuantity(name="U")

Now we have to add the calculation(Dynamics.c):

CudaDeviceFunction real_t getU() {
  return u(0,0);
}

Running a case

Now we need to create a case file (let's call it example.xml):

<?xml version="1.0"?>
<CLBConfig output="output/">
        <Geometry nx="128" ny="128">
    </Geometry>
    <Model>
    </Model>
    <VTK Iterations="10"/>
    <Solve Iterations="1000"/>
</CLBConfig>

This case will create a mesh of 128x128 nodes, initialize it and run 1000 iterations. It will also save VTK output every 10 iterations.

In order to run it:

make configure
./configure --enable-graphics
make wave
CLB/wave/main example.xml

The results are not so impressive now, because basically, not only nothing is happening in a node, but also it is initialized with 0.

Settings

Let us introduce two settings to our model(Dynamics.R):

AddSetting(name="Speed")
AddSetting(name="Value", zonal=TRUE)

Where Speed will be our parameter k in the wave equation, and Value will be the initial value of u. [[Settings]] which we want to be changing in the domain, are called "zonal". Settings are provided to us as variables in Dynamics.c. Additionally, we need to modify Color function to observe the change in values in preview window:

CudaDeviceFunction float2 Color() {
  float2 ret;
  ret.x = getU();
  ret.y = 1;
  return ret;
}

CudaDeviceFunction void Init() {
  u = Value;
  v = 0;
}

Now we can name a region in our domain, and initialize it with a different value:

<?xml version="1.0"?>
<CLBConfig output="output/">
  <Geometry nx="128" ny="128">
    <None name="box">
      <Box dx="60" nx="20" dy="20" ny="30"/>
    </None>
  </Geometry>
  <Model>
    <Param name="Value" value="0"/>
    <Param name="Value" value="1" zone="box"/>
  </Model>
  <VTK Iterations="10"/>
  <Solve Iterations="1000"/>
</CLBConfig>

This will mark a box 20x30 starting from the point (60,20) as a zone called 'box'. Then in the <Model> we first set Value in all zones to 0, then set it to 1 in 'box'.

Notice: Don't forget to compile(make wave) the model again before running it after making any changes to Dynamics.c or Dynamics.R.

You will see that the results now are much more interesting. Ok. I'm joking, they are sill constant - but at least not 0.

Introducing FD

Now we want to introduce the discretisation of our wave equation in to the mix:

CudaDeviceFunction void Run() {
  real_t lap_u = u(-1,0) + u(1,0) + u(0,-1) + u(0,1) - 4*u(0,0);
  real_t a = Speed * Speed * lap_u;
  v = v(0,0) + a;
  u = u(0,0) + v;
}

You can see that we assumed dx and dt equal to 1 (it will be more clear why, later on).

And now ... it won't compile. Why? The error is a bit obscure, like with many C++ Templates errors, but the reason is simple. We didn't tell the code that we want to access u in our neighbors. This is crucial, because the code have to know exactly were things are accessed, to prepare the right communication buffers. You can imagine that the neighboring node is on a different GPU on a different computer. Then we need this computer to know that it will have to send this data to us. On the other hand we want to send as small packets of information as possible, that is why the code have to be conservative wrt. to the possible access patterns. We define this information in Dynamics.R:

AddField(name="u", dx=c(-1,1), dy=c(-1,1))

If you don't know R then you need to know that c(...) means a vector/table of numbers. The above line means that the field u can be accessed for dx from -1 to 1 and dy from -1 to 1. Making it simple: we can access it from all of our 8 neighbors and ourselves. The other way (a shortcut) to express it would be:

AddField(name="u", stencil2d=1)

Which means the same thing (stencil3d would mean also -1 to 1 in z direction)

Now, the code compiles. We can add another parameter

<Param name="Speed" value="0.05" />

to our case file, run and see how the wave propagates.

Make it nicer:

We see that the result isn't very beautiful. It is partly because of our discretization, partly because the Fourier transform of a rectangle isn't very nice. Let us introduce viscosity/drag to the system:

CudaDeviceFunction void Run() {
  real_t lap_u = u(-1,0) + u(1,0) + u(0,-1) + u(0,1) - 4*u(0,0);
  real_t lap_v = v(-1,0) + v(1,0) + v(0,-1) + v(0,1) - 4*v(0,0);
  real_t a = Speed * Speed * lap_u + Viscosity * lap_v;
  v = v(0,0) + a;
  u = u(0,0) + v;
}

Remember: you have to modify the v field access pattern, and add a Viscosity setting in Dynamics.R.

Now you can play a bit with the settings to see some nice waves propagating. It can be seen now more clearly that the domain in TCLB is always periodic. That is simply because it is the most general case. If you want to make your domain non-periodic - you must add boundary conditions - otherwise, whatever leaves on one side - comes back on the other.

Node types

Now we can add node types that will change the behavior of some, selected nodes. For instance, let us have a Dirichlet boundary condition. We want the nodes that are on the boundary to set u and v to a fixed value. Let's call such nodes Dirichlet. We define a new node type (yes, you guessed: in Dynamics.R):

AddNodeType(name="Dirichlet", group="BOUNDARY")

You can notice that node types have 'groups' (note: these groups, customary are with all caps). Each node can only be of one type ... from each group. You can imagine it like this: in each node we want to be able to set separately a boundary condition, choose a discretization model and add a heat source. But you cannot set two boundary conditions in the same node, from the same group.

Now, when we have this node type, we can use it to change the dynamics:

CudaDeviceFunction void Run() {
  real_t lap_u = u(-1,0) + u(1,0) + u(0,-1) + u(0,1) - 4*u(0,0);
  real_t lap_v = v(-1,0) + v(1,0) + v(0,-1) + v(0,1) - 4*v(0,0);
  real_t a = Speed * Speed * lap_u + Viscosity * lap_v;
  v = v(0,0) + a;
  u = u(0,0) + v;
  if ((NodeType & NODE_BOUNDARY) == NODE_Dirichlet) {
    u = Value;
    v = 0;
  }
}

You can notice that we re-used the same zonal setting Value in this boundary condition. You can also notice, that the main calculation is still executed in the Dirichlet nodes. You can test it and see which version runs faster. Such additional computation can sometimes have a favorable impact on the performance on GPU, because of thing called branching.

Now, we can set some Dirichlet elements in the case file:

<?xml version="1.0"?>
<CLBConfig output="output/">
  <Geometry nx="128" ny="128">
      <Dirichlet name="border">
        <Box nx="1"/>
        <Box dx="-1"/>
        <Box ny="1"/>
        <Box dy="-1"/>
      </Dirichlet>
      <None name="box">
        <Box dx="60" nx="20" dy="20" ny="30"/>
      </None>
  </Geometry>
  <Model>
    <Param name="Value" value="0"/>
    <Param name="Value" value="1" zone="box"/>
    <Param name="Value" value="0" zone="border"/>
    <Param name="Speed" value="0.05"/>
    <Param name="Viscosity" value="0.001"/>
  </Model>
  <VTK Iterations="10"/>
  <Solve Iterations="10000"/>
</CLBConfig>

We can notice the difference immediately. The waves are bouncing from the walls now.

In this case, we had a simple situation, as we have only one group of node types (and only one type), but normally we would have to distinguish between them. It would be done with:

if ((NodeType & NODE_BOUNDARY) == NODE_Dirichlet) {
  ...
}

or

switch (NodeType & NODE_BOUNDARY) {
  case NODE_Dirichlet:
  ...
  break;
  case ...:
  ...
}