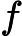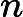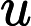D2Q9 Shan-Chen SRT
Introduction
This tutorial will teach you how to use lattice Boltzmann method (LBM) to simulate a simple single-component multi-phase system with a contact angle within the TCLB environment. It is assumed that the you have already completed the previous tutorial, namely 'D2Q9 Single Relaxation Time'. The source code of completed 'D2Q9 Single Relaxation Time' tutorial is here.
First, a brief repetition of SRT and overview of the Schan-Chen model (AKA Pseudo Potential) lattice Boltzmann equation will be given. Then, we will code the model step by step.
The SRT-lattice Boltzmann Equation:
As in the previous example, the discrete form of the Boltzmann transport equation is expressed as:
This describes the evolution of particle distribution functions along discrete velocities, where the right hand side is often referred to as the collision operation and the evaluation to the left hand side, the streaming operation. Note here that we are going to work in lattice units during the description of the model in which we assume . For the D2Q9 model, this assumption allows us to express the 9 discrete directions as,
Additionally, we define the equilibrium distribution function found by an expansion of a Maxwellian distribution as,
where,
Boundary Conditions
In this tutorial we will investigate a droplet in a box.
The box is defined by no-slip wall boundary conditions. To do this with LBM, the bounceback method is used. In this, particle distribution functions that stream into a node flagged as a "wall" are reversed, or "bounced-back" in the direction they came. Therefore, in general for a D2Q9 lattice we obtain:
where the ' indicates the post-bounce-back direction. You can observe that
Force Implementation
The pseudo-potential model uses a “bottom-up” approach. This mean, that the microscopic interaction between fluid elements is postulated, which results in the macroscopic separation of phases. Depending on the 'postulation' different Equations Of State can be achieved.
Without digging into details, the pseudo-potential field is frequently defined as:
Then, the fluid - fluid interaction force follows by:
where is a scalar used t adjust interaction strength.
Starting from Newton's second law we can account for the presence of force by incorporating it into equlibrium momentum.
If there are more forces (like Gravity, Fluid-Fluid and Solid-Fluid interaction), we can simply sum them into F :
This approach ultimately acts to relax each particle distribution function towards an equilibrium momentum that has included the time-incremental change due to the applied body force. To obtain the bulk fluid velocity, the before and after collision momentum is averaged giving,
and with this we have all we the dynamics required to implement the specified example.
Model Creation in TCLB
Dynamics.R
As per the FD wave equation tutorial, we want to set up a folder named 'my_d2q9_ShanChen' in the /models/ folder within TCLB. Additionally, the generic file structure needs to be created consisting of conf.mk, Dynamics.c, Dynamics.R.
To start off the model, we look to add the nine distribution functions for the nine discrete velocities. This is implemented in the Dynamics.R file, but instead of adding each as its own field we look to stream the functions in the process of calling them at each node. To do this we instead add them as Densities:
# Fluid Density Populations
AddDensity( name="f[0]", dx= 0, dy= 0, group="f")
AddDensity( name="f[1]", dx= 1, dy= 0, group="f")
AddDensity( name="f[2]", dx= 0, dy= 1, group="f")
AddDensity( name="f[3]", dx=-1, dy= 0, group="f")
AddDensity( name="f[4]", dx= 0, dy=-1, group="f")
AddDensity( name="f[5]", dx= 1, dy= 1, group="f")
AddDensity( name="f[6]", dx=-1, dy= 1, group="f")
AddDensity( name="f[7]", dx=-1, dy=-1, group="f")
AddDensity( name="f[8]", dx= 1, dy=-1, group="f")
AddDensity( name="rho", dx=0, dy=0, group="density")
We add the density rho since it will be used frequently and we don't want evaluate it each time.
Then we add pseudopotential field psi and one more neighbour_type field which will be used to distinguish whether neighbouring cell is a fluid or a wall.
# Pseudopotential field
AddField("psi", stencil2d=1, group="pp")
AddField("neighbour_type", stencil2d=1, group="neighbour_type_group")
Next we will define 'Initialization list' and 'Iteration list'. Each iteration consists of two stages, one resposible for update of 'f' populations and the other one used to calculate the 'psi' field.
# Stages and Actions
# Initialization list
AddStage("BaseInit" , "Init", save=Fields$group %in% c("f", "density", "neighbour_type_group"), load=DensityAll$group%in% c("f","density"))
# Iteration list
AddStage("BaseIteration", "Run" , save=Fields$group %in% c("f", "density", "neighbour_type_group") , load=DensityAll$group %in% c("f","density","neighbour_type_group"))
AddStage("PsiIteration" , "calcPsi" , save=Fields$name=="psi", load=DensityAll$group %in% c("f", "density"))
AddAction("Init" , c("BaseInit", "PsiIteration"))
AddAction("Iteration", c("BaseIteration", "PsiIteration"))
caveat
caveat
In TCLB core there is buffer 'A' and 'B'. During each iteration it switches the values from 'A' to 'B' and vice-versa. Thus if you save 'x' only during initialization you will see the old value of 'x' coming back each second iteration.
To fix it he have to add the 'save' command during each iteration in Dynamics.R
Simalarly, in Dynamics.c the 'x' must saved during execution of Run() function like x = x(0,0), but we will come back to it later.
This is the reason why we have to save the neighbour_type_group during the BaseIteration even if its value is not changed.
Finally we can define the output variables:
# Output Values
AddQuantity( name="U", unit="m/s", vector=TRUE )
AddQuantity( name="Rho", unit="kg/m3" )
AddQuantity( name="Psi", unit="1" )
And parameters used as input:
# Model Specific Parameters
AddSetting( name="omega", comment='inverse of relaxation time')
AddSetting( name="viscosity", omega='1.0/(3*viscosity+0.5)', default=0.16666666, comment='kinematic viscosity')
AddSetting( name="VelocityX",default=0, comment='inlet/outlet/init velocity', zonal=TRUE)
AddSetting( name="VelocityY",default=0, comment='inlet/outlet/init velocity', zonal=TRUE)
AddSetting( name="GravitationX",default=0, comment='body/external acceleration', zonal=TRUE)
AddSetting( name="GravitationY",default=0, comment='body/external acceleration', zonal=TRUE)
AddSetting( name="Density",default=1, comment='Density',zonal=TRUE)
AddSetting( name="G_ff",default=0, comment='fluid-fluid interaction strength')
AddSetting( name="G_sf",default=0, comment='solid-fluid interaction strength')
Dynamics.c
From the above, we have all the variables we need to implement the LBM.
Before start, we need to load dependecies:
<?R
source("conf.R")
c_header();
source("lib/feq.R")
source("lib/boundary.R")
?>
The first step is to initialise the lattice over the required domain, this is incorporated as part of the dynamics that are occurring in the model and must be incorporated into the Dynamics.c file within the Init() function.
CudaDeviceFunction void Init(){
real_t u[2] = {VelocityX, VelocityY};
real_t d = Density;
SetEquilibrium(d,u);
rho = calcRho(); // calculate rho from equilibrium distributions.
neighbour_type=0;
if ((NodeType & NODE_BOUNDARY) == NODE_Wall) {
neighbour_type=1;
}
}
To deal with density we implent calcRho() and getRho()
CudaDeviceFunction real_t calcRho() {
// This function calculates and returns the value of macroscopic density at the current node.
real_t d = f[8]+f[7]+f[6]+f[5]+f[4]+f[3]+f[2]+f[1]+f[0];
return d;
}
CudaDeviceFunction real_t getRho() {
// This function returnes the stored value of macroscopic density at the current node.
return rho;
}
Same as in previous tutorial, we are calling on the function SetEquilibrium() within which we want to calculate the equilibrium distribution for the given density and velocity fields.
CudaDeviceFunction void SetEquilibrium(real_t d, real_t u[2])
{
f[0] = ( 2. + ( -u[1]*u[1] - u[0]*u[0] )*3. )*d*2./9.;
f[1] = ( 2. + ( -u[1]*u[1] + ( 1 + u[0] )*u[0]*2. )*3. )*d/18.;
f[2] = ( 2. + ( -u[0]*u[0] + ( 1 + u[1] )*u[1]*2. )*3. )*d/18.;
f[3] = ( 2. + ( -u[1]*u[1] + ( -1 + u[0] )*u[0]*2. )*3. )*d/18.;
f[4] = ( 2. + ( -u[0]*u[0] + ( -1 + u[1] )*u[1]*2. )*3. )*d/18.;
f[5] = ( 1. + ( ( 1 + u[1] )*u[1] + ( 1 + u[0] + u[1]*3. )*u[0] )*3. )*d/36.;
f[6] = ( 1. + ( ( 1 + u[1] )*u[1] + ( -1 + u[0] - u[1]*3. )*u[0] )*3. )*d/36.;
f[7] = ( 1. + ( ( -1 + u[1] )*u[1] + ( -1 + u[0] + u[1]*3. )*u[0] )*3. )*d/36.;
f[8] = ( 1. + ( ( -1 + u[1] )*u[1] + ( 1 + u[0] - u[1]*3. )*u[0] )*3. )*d/36.;
}
With the equilibrium function taken care of, we can now look at updating our initialised lattice. For this, the streaming operation is taken care of with the specification of Densities that we made. The collision operation however needs to be implemented and bounce-back for nodes flagged as walls. To do this, we define the run() function to describe what happens at each node at each timestep.
CudaDeviceFunction void Run() {
// This defines the dynamics that we run at each node in the domain.
rho = calcRho();
switch (NodeType & NODE_BOUNDARY) {
case NODE_Solid:
case NODE_Wall:
BounceBack();
break;
}
if (NodeType & NODE_MRT)
{
CollisionBGK();
}
neighbour_type = neighbour_type(0,0);
}
Here is the line neighbour_type = neighbour_type(0,0); which was discussed in the caveat.
Same as in D2Q9 SRT Tutorial, we need to define functions that describe both the BounceBack() and CollisionBGK() operations. The bounce-back operation occurs as described in the theory component of this tutorial where distribution functions are reversed:
CudaDeviceFunction void BounceBack() {
// Method to reverse distribution functions along the bounding nodes.
real_t uf;
uf = f[3];
f[3] = f[1];
f[1] = uf;
uf = f[4];
f[4] = f[2];
f[2] = uf;
uf = f[7];
f[7] = f[5];
f[5] = uf;
uf = f[8];
f[8] = f[6];
f[6] = uf;
}
While the BGK collision involved implementing the left hand side of the discrete Boltzmann equation.
// Here we perform a single relaxation time collision operation.
// We save memory here by using a single dummy variable
real_t u_eq[2], f_temp[9];
real_t d = getRho();
vector_t u_eq_vect = getUeq(d);
u_eq[0] = u_eq_vect.x;
u_eq[1] = u_eq_vect.y;
f_temp[0] = f[0];
f_temp[1] = f[1];
f_temp[2] = f[2];
f_temp[3] = f[3];
f_temp[4] = f[4];
f_temp[5] = f[5];
f_temp[6] = f[6];
f_temp[7] = f[7];
f_temp[8] = f[8];
SetEquilibrium(d, u_eq); //stores equilibrium distribution in f[0]-f[8]
f[0] = f_temp[0] - omega*(f_temp[0]-f[0]);
f[1] = f_temp[1] - omega*(f_temp[1]-f[1]);
f[2] = f_temp[2] - omega*(f_temp[2]-f[2]);
f[3] = f_temp[3] - omega*(f_temp[3]-f[3]);
f[4] = f_temp[4] - omega*(f_temp[4]-f[4]);
f[5] = f_temp[5] - omega*(f_temp[5]-f[5]);
f[6] = f_temp[6] - omega*(f_temp[6]-f[6]);
f[7] = f_temp[7] - omega*(f_temp[7]-f[7]);
f[8] = f_temp[8] - omega*(f_temp[8]-f[8]);
}
In this model we will use the Schan-Chen forcing shceme, which says the forcing term has to be added to the equibrium velocity.
We calculate the equilibrium velocity by:
CudaDeviceFunction vector_t getUeq() {
real_t d = getRho();
vector_t F_ff = getF_ff();
vector_t F_sf = getF_sf();
vector_t u_eq;
u_eq.x = ( f[8]-f[7]-f[6]+f[5]-f[3]+f[1] )/d;
u_eq.y = (-f[8]-f[7]+f[6]+f[5]-f[4]+f[2] )/d;
u_eq.x += (GravitationX + (F_ff.x + F_sf.x)/d) / omega;
u_eq.y += (GravitationY + (F_ff.y + F_sf.y)/d) / omega;
u_eq.z = 0;
return u_eq;
}
To display the actual velocity we use:
CudaDeviceFunction vector_t getU() {
// This function defines the macroscopic velocity at the current node.
real_t d = getRho();
vector_t u;
vector_t F_ff = getF_ff();
vector_t F_sf = getF_sf();
u.x = ( f[8]-f[7]-f[6]+f[5]-f[3]+f[1] )/d + (GravitationX + F_ff.x + F_sf.x )*0.5 ;
u.y = (-f[8]-f[7]+f[6]+f[5]-f[4]+f[2] )/d + (GravitationY + F_ff.y + F_sf.y )*0.5 ;
u.z = 0;
return u;
}
Forces
Next step is to define the forcing functions. First, we have to find the pseudopotential field:
CudaDeviceFunction void calcPsi() {
// Calculate psi at each point so that pseudopotential force can be found.
// eq 9.102 p369 from book: 'The Lattice Boltzmann Method: Principles and Practice'
// T. Krüger, H. Kusumaatmaja, A. Kuzmin, O. Shardt, G. Silva, E.M. Viggen
real_t rho = getRho();
psi = 1 - exp(-rho);
}
The fluid - fluid interaction force is given by:
where is a scalar used t adjust interaction strength.
CudaDeviceFunction vector_t getF_ff() {
// fluid - fluid interaction force
// eq 9.105 p 372 from book: 'The Lattice Boltzmann Method: Principles and Practice'
// T. Krüger, H. Kusumaatmaja, A. Kuzmin, O. Shardt, G. Silva, E.M. Viggen
vector_t F_ff;
F_ff.x = 0;
F_ff.y = 0;
F_ff.z = 0;
F_ff.x = ( psi(1,-1)-psi(-1,-1)+psi(1,1)-psi(-1,1))/9. + (psi(1,0)-psi(-1,0))/36.;
F_ff.y = (-psi(1,-1)-psi(-1,-1)+psi(1,1)+psi(-1,1))/9. + (psi(0,1)-psi(0,-1))/36.;
F_ff.x *= -G_ff*psi(0,0);
F_ff.y *= -G_ff*psi(0,0);
// alternative version with dynamic access to the 'psi' field.
// for (int i=0; i< 9; i++){
// F_ff.x += wf[i] * psi_dyn(d2q9_ex[i], d2q9_ey[i])*d2q9_ex[i];
// F_ff.y += wf[i] * psi_dyn(d2q9_ex[i], d2q9_ey[i])*d2q9_ey[i];
// }
return F_ff;
}
The solid-fluid force can be expressed in a similar manner:
Playing with the values of one can find a desired contact angle. Unfortunately there is no straighforward method to know the value of without numerical experiments.
The is a switch function used to distiguish fluid and solid nodes. It takes a value of 1 for solid-fluid interaction and 0 when neighbouring nodes are both fluid. In TCLB, simpest way (not necessary most efficient) to realize it is to add additional field in Dynamics.R
AddField("neighbour_type", stencil2d=1, group="neighbour_type_group")
Then, we have to prescribe the value in the initialization step
CudaDeviceFunction void Init(){
real_t u[2] = {VelocityX, VelocityY};
real_t d = Density;
SetEquilibrium(d,u);
neighbour_type=0;
if ((NodeType & NODE_BOUNDARY) == NODE_Wall) {
neighbour_type=1;
}
}
Finally, we can code the solid-fluid force:
CudaDeviceFunction vector_t getF_sf() {
// fluid - solid interaction force
// eq 9.116 p376 from book: 'The Lattice Boltzmann Method: Principles and Practice'
// T. Krüger, H. Kusumaatmaja, A. Kuzmin, O. Shardt, G. Silva, E.M. Viggen
vector_t F_sf;
F_sf.x = 0;
F_sf.y = 0;
F_sf.z = 0;
for (int i=0; i< 9; i++){
F_sf.x += wf[i] *d2q9_ex[i] * neighbour_type_dyn(d2q9_ex[i], d2q9_ey[i]);
F_sf.y += wf[i] *d2q9_ey[i] * neighbour_type_dyn(d2q9_ex[i], d2q9_ey[i]);
}
F_sf.x *= -G_sf*psi(0,0);
F_sf.y *= -G_sf*psi(0,0);
return F_sf;
}
The some_field_dyn access pattern is used here to get the field value from neighbouring node.
Setting up a Simulation
Create a configuration file, my_pp_config.xml in example/
<?xml version="1.0"?>
<CLBConfig output="output/">
<Geometry nx="128" ny="128">
<MRT><Box/></MRT>
<Wall mask="ALL" name="border" >
<Box nx="1"/>
<Box dx="-1"/>
<Box ny="1"/>
<Box dy="-1"/>
</Wall>
<None name="blobb">
<!-- <Box dx="50" nx="28" dy="50" ny="28"/> -->
<Sphere ny="48" nx="48" dx="40" dy="0" />
</None>
</Geometry>
<Model>
<Param name="Density" value="0.056"/>
<Param name="Density" value="2.659" zone="blobb"/>
<Param name="G_ff" value="-6.0"/>
<Param name="G_sf" value="-2.7"/>
<Param name="viscosity" value="0.166"/>
<!-- <Params name="GravitationY" value="-1e-5"/> -->
</Model>
<Solve Iterations="100" output="output/"> <VTK Iterations="1"/> </Solve>
<Solve Iterations="1000" output="output/"> <VTK Iterations="10"/> </Solve>
<Failcheck Iterations="1000" />
<Solve Iterations="10000" output="output/"> <VTK Iterations="500"/> </Solve>
</CLBConfig>
You can play with the configuration file, for example switching from
With the model and set-up files created, we can now look to make and run my_d2q9_ShanChen.
Enter the TCLB directory and call the run file along with the input file location, after this, the analysis can be performed in Paraview:
make my_d2q9_ShanChen
CLB/my_d2q9_ShanChen/main example/multiphase/ShanChen/my_d2q9_sc.xml
paraview output/my_pp_config_VTK_P00_..pvti
To run in parallel an mpi run can also be initiated:
mpirun -np 8 CLB/my_d2q9_ShanChen/main example/multiphase/ShanChen/my_d2q9_sc.xml
It it interesting to observe that the droplet shrinks and extends before reaching the steady state.
Even then, you can observe so called pasasitic currents being a numerical artefact. Sometimes, they can be so large that the droplet will move!
References
Tip
A good starting point explaining the 'zoology' of various LBM models is a modern (2017) book 'The Lattice Boltzmann Method: Principles and Practice' written by T. Krüger, H. Kusumaatmaja, A. Kuzmin, O. Shardt, G. Silva, E.M. Viggen .
The pseudo potential model comes from the work of X. Shan and H. Chen:
X. Shan, H. Chen, Phys. Rev. E 47(3), 1815 (1993)
X. Shan, G. Doolen, J. Stat. Phys. 81(1), 379 (1995)